UNIT-1 (CHAPTER-1 FUNDAMENTALS) THEORY OF COMPUTATION

SKYSPIN

UNIT-1 (CHAPTER-1 FUNDAMENTALS OF TOC)

Introduction of Theory of Computation

Automata theory (also known as Theory Of Computation) is a theoretical branch of Computer Science and Mathematics, which mainly deals with the logic of computation with respect to simple machines, referred to as automata.Automata* enables the scientists to understand how machines compute the functions and solve problems. The main motivation behind developing Automata Theory was to develop methods to describe and analyse the dynamic behavior of discrete systems.
Automata is originated from the word “Automaton” which is closely related to “Automation”.

Theory of Computation:

• Is one of the most fundamental courses of Computer Science
• Will help you understand how people have thought about Computer Science as a Science in the past 50 years
• Is mainly about what kind of things can you really compute mechanically, how fast can you do it and how much space does it take to do so.

Example:

Can we design a machine that accepts all binary strings that end in ${}^{}{0}^{\prime }$
?
→ YES we can. The machine can easily scan the last digit and decide whether it is $0$
or $1$ and can accept the string if it happens to end with $0$ 2. Can we design a machine that accepts all valid JAVA codes?
→ YES we can. The COMPILERS that we use are the best example for this and they do the exact same thing.
Can we design a machine that accepts all valid JAVA codes and NEVER GOES INTO AN INFINITE LOOP?
→ NO we can’t. It is not possible to design a machine that will never allow a code to go into infinite loop.
The basic idea of this subject is depicted using the figure below. We give an input to the machine/ system that we design and the machine either accepts or rejects the input based on some predefined rules

Layers / Levels of the Subject that will be studied:

Now, let’s understand the basic terminologies, which are important and frequently used in Theory of Computation.

• Symbol: Symbol is the smallest building block, which can be any alphabet, letter or any picture.
  


• Alphabets (Σ): Alphabets are set of symbols, which are always finite.
  


• String: String is a finite sequence of symbols from some alphabet. String is generally denoted as w and length of a string is denoted as |w|. 

• Note – If the number of Σ’s is represented by |Σ|, then number of strings of length n, possible over Σ is |Σ|ⁿ.


• Language: A language is a set of strings, chosen from some Σ* or we can say- ‘A language is a subset of Σ* ‘. A language which can be formed over ‘ Σ ‘ can be Finite or Infinite.

Powers of ‘ Σ ‘ :
Say Σ = {a,b} then
Σ⁰ = Set of all strings over Σ of length 0. {ε}
Σ¹ = Set of all strings over Σ of length 1. {a, b}
Σ² = Set of all strings over Σ of length 2. {aa, ab, ba, bb}
i.e. |Σ²|= 4 and Similarly, |Σ³| = 8
 

Applications of various Automata

Automata is a machine that can accept the Strings of a Language L over an input alphabet .So far we are familiar with the Types of Automata . Now, let us discuss the expressive power of Automata and further understand its Applications.
Expressive Power of various Automata:
The Expressive Power of any machine can be determined from the class or set of Languages accepted by that particular type of Machine. Here is the increasing sequence of expressive power of machines :


The Applications of these Automata are given as follows:
1. Finite Automata (FA) –

• For the designing of lexical analysis of a compiler.
• For recognizing the pattern using regular expressions.
• For the designing of the combination and sequential circuits using Mealy and Moore Machines.
• Used in text editors.
• For the implementation of spell checkers.

2. Push Down Automata (PDA) –

• For designing the parsing phase of a compiler (Syntax Analysis).
• For implementation of stack applications.
• For evaluating the arithmetic expressions.
• For solving the Tower of Hanoi Problem.

3. Linear Bounded Automata (LBA) –

• For implementation of genetic programming.
• For constructing syntactic parse trees for semantic analysis of the compiler.

4. Turing Machine (TM) –

• For solving any recursively enumerable problem.
• For understanding complexity theory.
• For implementation of neural networks.
• For implementation of Robotics Applications.
• For implementation of artificial intelligence. 

Finite Automata

• Finite automata are used to recognize patterns.
• It takes the string of symbol as input and changes its state accordingly. When the desired symbol is found, then the transition occurs.
• At the time of transition, the automata can either move to the next state or stay in the same state.
• Finite automata have two states, Accept state or Reject state. When the input string is processed successfully, and the automata reached its final state, then it will accept.

Formal Definition of FA

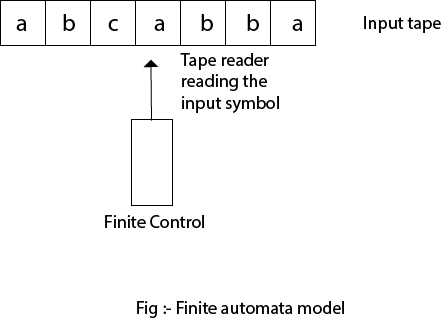
A finite automaton is a collection of 5-tuple (Q, ∑, δ, q0, F), where:

Finite Automata Model:

Finite automata can be represented by input tape and finite control.
Input tape: It is a linear tape having some number of cells. Each input symbol is placed in each cell.

Finite control: The finite control decides the next state on receiving particular input from input tape. The tape reader reads the cells one by one from left to right, and at a time only one input symbol is read.

Types of Automata:

There are two types of finite automata:

1. DFA(deterministic finite automata)
2. NFA(non-deterministic finite automata)

1. DFA
DFA refers to deterministic finite automata. Deterministic refers to the uniqueness of the computation. In the DFA, the machine goes to one state only for a particular input character. DFA does not accept the null move.
2. NFA
NFA stands for non-deterministic finite automata. It is used to transmit any number of states for a particular input. It can accept the null move.
Some important points about DFA and NFA:

1. Every DFA is NFA, but NFA is not DFA.
2. There can be multiple final states in both NFA and DFA.
3. DFA is used in Lexical Analysis in Compiler.
4. NFA is more of a theoretical concept.

Transition Diagram

A transition diagram or state transition diagram is a directed graph which can be constructed as follows:

• There is a node for each state in Q, which is represented by the circle.
• There is a directed edge from node q to node p labeled a if δ(q, a) = p.
• In the start state, there is an arrow with no source.
• Accepting states or final states are indicating by a double circle.

Some Notations that are used in the transition diagram:

There is a description of how a DFA operates:

1. In DFA, the input to the automata can be any string. Now, put a pointer to the start state q and read the input string w from left to right and move the pointer according to the transition function, δ. We can read one symbol at a time. If the next symbol of string w is a and the pointer is on state p, move the pointer to δ(p, a). When the end of the input string w is encountered, then the pointer is on some state F.
2. The string w is said to be accepted by the DFA if r ∈ F that means the input string w is processed successfully and the automata reached its final state. The string is said to be rejected by DFA if r ∉ F.

Example 1:

DFA with ∑ = {0, 1} accepts all strings starting with 1.
Solution:

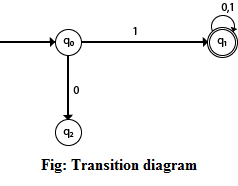
The finite automata can be represented using a transition graph. In the above diagram, the machine initially is in start state q0 then on receiving input 1 the machine changes its state to q1. From q0 on receiving 0, the machine changes its state to q2, which is the dead state. From q1 on receiving input 0, 1 the machine changes its state to q1, which is the final state. The possible input strings that can be generated are 10, 11, 110, 101, 111......., that means all string starts with 1.

Example 2:

NFA with ∑ = {0, 1} accepts all strings starting with 1.
Solution:

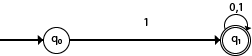
The NFA can be represented using a transition graph. In the above diagram, the machine initially is in start state q0 then on receiving input 1 the machine changes its state to q1. From q1 on receiving input 0, 1 the machine changes its state to q1. The possible input string that can be generated is 10, 11, 110, 101, 111......, that means all string starts with 1.

DFA (Deterministic finite automata)

• DFA refers to deterministic finite automata. Deterministic refers to the uniqueness of the computation. The finite automata are called deterministic finite automata if the machine is read an input string one symbol at a time.
• In DFA, there is only one path for specific input from the current state to the next state.
• DFA does not accept the null move, i.e., the DFA cannot change state without any input character.
• DFA can contain multiple final states. It is used in Lexical Analysis in Compiler.

In the following diagram, we can see that from state q0 for input a, there is only one path which is going to q1. Similarly, from q0, there is only one path for input b going to q2.

Formal Definition of DFA

A DFA is a collection of 5-tuples same as we described in the definition of FA.
  Transition function can be defined as:
 

Graphical Representation of DFA

A DFA can be represented by digraphs called state diagram. In which:

1. The state is represented by vertices.
2. The arc labeled with an input character show the transitions.
3. The initial state is marked with an arrow.
4. The final state is denoted by a double circle.

Example 1:

  

Solution:
Transition Diagram:

Transition Table:
 

Example 2:

DFA with ∑ = {0, 1} accepts all starting with 0.
Solution:

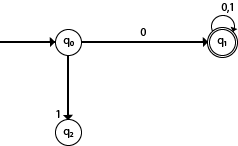
Explanation:

• In the above diagram, we can see that on given 0 as input to DFA in state q0 the DFA changes state to q1 and always go to final state q1 on starting input 0. It can accept 00, 01, 000, 001....etc. It can't accept any string which starts with 1, because it will never go to final state on a string starting with 1.

Example 3:

DFA with ∑ = {0, 1} accepts all ending with 0.
Solution:

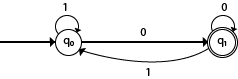
Explanation:
In the above diagram, we can see that on given 0 as input to DFA in state q0, the DFA changes state to q1. It can accept any string which ends with 0 like 00, 10, 110, 100....etc. It can't accept any string which ends with 1, because it will never go to the final state q1 on 1 input, so the string ending with 1, will not be accepted or will be rejected.

NFA (Non-Deterministic finite automata)

• NFA stands for non-deterministic finite automata. It is easy to construct an NFA than DFA for a given regular language.
• The finite automata are called NFA when there exist many paths for specific input from the current state to the next state.
• Every NFA is not DFA, but each NFA can be translated into DFA.
• NFA is defined in the same way as DFA but with the following two exceptions, it contains multiple next states, and it contains ε transition.

In the following image, we can see that from state q0 for input a, there are two next states q1 and q2, similarly, from q0 for input b, the next states are q0 and q1. Thus it is not fixed or determined that with a particular input where to go next. Hence this FA is called non-deterministic finite automata.

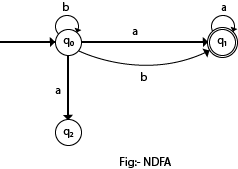
Formal definition of NFA:

NFA also has five states same as DFA, but with different transition function, as shown follows:
 
where,
 

Graphical Representation of an NFA

An NFA can be represented by digraphs called state diagram. In which:

1. The state is represented by vertices.
2. The arc labeled with an input character show the transitions.
3. The initial state is marked with an arrow.
4. The final state is denoted by the double circle.

Example 1:

  

Solution:
Transition diagram:

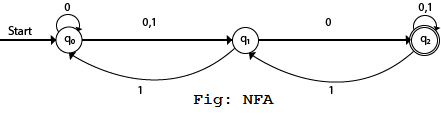
Transition Table:
 
In the above diagram, we can see that when the current state is q0, on input 0, the next state will be q0 or q1, and on 1 input the next state will be q1. When the current state is q1, on input 0 the next state will be q2 and on 1 input, the next state will be q0. When the current state is q2, on 0 input the next state is q2, and on 1 input the next state will be q1 or q2.

Example 2:

NFA with ∑ = {0, 1} accepts all strings with 01.
Solution:

Transition Table:
 

Example 3:

NFA with ∑ = {0, 1} and accept all string of length atleast 2.
Solution:
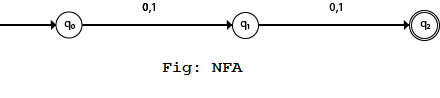Transition Table:
 

DFA vs NDFA

The following table lists the differences between DFA and NDFA.

 

---