SKYSPIN
In a regular expression, x* means zero or more occurrence of x. It can generate {e, x, xx, xxx, xxxx, .....}
In a regular expression, x+ means one or more occurrence of x. It can generate {x, xx, xxx, xxxx, .....}
Union: If L and M are two regular languages then their union L U M is also a union.

Intersection: If L and M are two regular languages then their intersection is also an intersection.

Kleen closure: If L is a regular language then its Kleen closure L1* will also be a regular language.

Solution:
All combinations of a's means a may be zero, single, double and so on. If a is appearing zero times, that means a null string. That is we expect the set of {ε, a, aa, aaa, ....}. So we give a regular expression for this as:

That is Kleen closure of a.
Solution:
The regular expression has to be built for the language

This set indicates that there is no null string. So we can denote regular expression as:

Solution:
The regular expression will be:

This will give the set as L = {ε, a, aa, b, bb, ab, ba, aba, bab, .....}, any combination of a and b.
The (a + b)* shows any combination with a and b even a null string.
Proof −
Let us take two regular expressions
and L2 ={ ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
Property 2. The intersection of two regular set is regular.
Proof −
Let us take two regular expressions
Property 3. The complement of a regular set is regular.
Proof −
Let us take a regular expression −
Complement of L is all the strings that is not in L.
So, L’ = {a, aaa, aaaaa, .....} (Strings of odd length excluding Null)
Property 4. The difference of two regular set is regular.
Proof −
Let us take two regular expressions −
Property 5. The reversal of a regular set is regular.
Proof −
We have to prove LR is also regular if L is a regular set.
Let, L = {01, 10, 11, 10}
Property 6. The closure of a regular set is regular.
Proof −
Hence, proved.
Property 7. The concatenation of two regular sets is regular.
Proof −
Let RE1 = (0+1)*0 and RE2 = 01(0+1)*
Here, L1 = {0, 00, 10, 000, 010, ......} (Set of strings ending in 0)
and L2 = {01, 010,011,.....} (Set of strings beginning with 01)
Then, L1 L2 = {001,0010,0011,0001,00010,00011,1001,10010,.............}
Set of strings containing 001 as a substring which can be represented by an RE − (0 + 1)*001(0 + 1)*
Hence, proved.
Step 1: Design a transition diagram for given regular expression, using NFA with ε moves.
Step 2: Convert this NFA with ε to NFA without ε.
Step 3: Convert the obtained NFA to equivalent DFA.
Solution: First we will construct the transition diagram for a given regular expression.
Step 1:
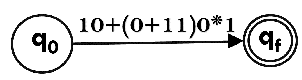
Step 2:
Step 3:
Step 4:
Step 5:
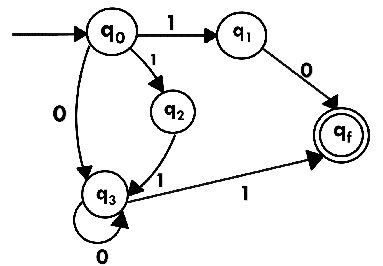
Now we have got NFA without ε. Now we will convert it into required DFA for that, we will first write a transition table for this NFA.

The equivalent DFA will be:

Solution: The NFA for the given regular expression is as follows:
Step 1:
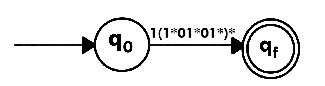
Step 2:
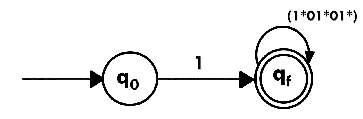
Step 3:
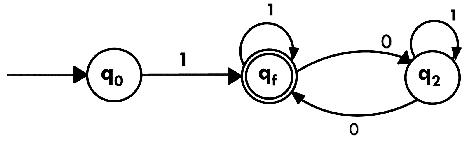
Solution:
We will first construct FA for R = 0*1 + 10 as follows:
Step 1:
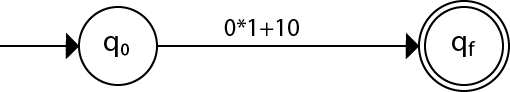
Step 2:
Step 3:
Step 4:
Arden’s theorem state that:
“If P and Q are two regular expressions over , and if P does not contain
, and if P does not contain  , then the following equation in R given by R = Q + RP has an unique solution i.e., R = QP*.”
, then the following equation in R given by R = Q + RP has an unique solution i.e., R = QP*.”
That means, whenever we get any equation in the form of R = Q + RP, then we can directly replaced by R = QP*. So, here first we will prove that R = QP* is the solution of this equation and then we will also prove that it is the unique solution of this equation.
Let’s start by taking this equation as equation (i)

Now, replacing R by R = QP*, we get,

Taking Q as common,

(As we know that + R*R = R*). Hence proved.
+ R*R = R*). Hence proved.
Thus, R = QP* is the solution of the equation R = Q + RP.
Now, we have to prove that this is the only solution of this equation. Let me take this equation again:

Now, replace R by R = Q + RP,

Again, replace R by R = Q + RP:-

Now, replace R by R = QP*, we get,

Taking Q as common,

Hence proved.
Thus, R = QP* is the unique solution of the equation R = Q + RP.
To understand this theorem, we will solve an example:
Example –

Now,

[Applying Arden’s theorem]. Hence, the value of q2 is 0*10*.
Output − Minimized DFA
Step 1 − Draw a table for all pairs of states (Qi, Qj) not necessarily connected directly [All are unmarked initially]
Step 2 − Consider every state pair (Qi, Qj) in the DFA where Qi ∈ F and Qj ∉ F or vice versa and mark them. [Here F is the set of final states]
Step 3 − Repeat this step until we cannot mark anymore states −
If there is an unmarked pair (Qi, Qj), mark it if the pair {δ (Qi, A), δ (Qi, A)} is marked for some input alphabet.
Step 4 − Combine all the unmarked pair (Qi, Qj) and make them a single state in the reduced DFA.
 Step 1 − We draw a table for all pair of states.
Step 1 − We draw a table for all pair of states.

Step 2 − We mark the state pairs.

Step 3 − We will try to mark the state pairs, with green colored check mark, transitively. If we input 1 to state ‘a’ and ‘f’, it will go to state ‘c’ and ‘f’ respectively. (c, f) is already marked, hence we will mark pair (a, f). Now, we input 1 to state ‘b’ and ‘f’; it will go to state ‘d’ and ‘f’ respectively. (d, f) is already marked, hence we will mark pair (b, f).

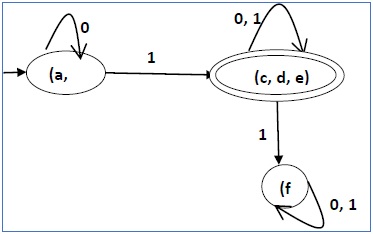
After step 3, we have got state combinations {a, b} {c, d} {c, e} {d, e} that are unmarked.
We can recombine {c, d} {c, e} {d, e} into {c, d, e}
Hence we got two combined states as − {a, b} and {c, d, e}
So the final minimized DFA will contain three states {f}, {a, b} and {c, d, e}
Step 2 − Increment k by 1. For each partition in Pk, divide the states in Pk into two partitions if they are k-distinguishable. Two states within this partition X and Y are k-distinguishable if there is an input S such that δ(X, S) and δ(Y, S) are (k-1)-distinguishable.
Step 3 − If Pk ≠ Pk-1, repeat Step 2, otherwise go to Step 4.
Step 4 − Combine kth equivalent sets and make them the new states of the reduced DFA.

Let us apply the above algorithm to the above DFA −
There are three states in the reduced DFA. The reduced DFA is as follows −

There are two Pumping Lemmas, which are defined for
1. Regular Languages, and
2. Context – Free Languages
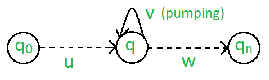
(1) |uv| ≤ n
(2) |v| ≥ 1
(3) for all i ≥ 0: uviw ∈ L
In simple terms, this means that if a string v is ‘pumped’, i.e., if v is inserted any number of times, the resultant string still remains in L.
Pumping Lemma is used as a proof for irregularity of a language. Thus, if a language is regular, it always satisfies pumping lemma. If there exists at least one string made from pumping which is not in L, then L is surely not regular.
The opposite of this may not always be true. That is, if Pumping Lemma holds, it does not mean that the language is regular.
For example, let us prove L01 = {0n1n | n ≥ 0} is irregular.
Let us assume that L is regular, then by Pumping Lemma the above given rules follow.
Now, let x ∈ L and |x| ≥ n. So, by Pumping Lemma, there exists u, v, w such that (1) – (3) hold.
We show that for all u, v, w, (1) – (3) does not hold.
If (1) and (2) hold then x = 0n1n = uvw with |uv| ≤ n and |v| ≥ 1.
So, u = 0a, v = 0b, w = 0c1n where : a + b ≤ n, b ≥ 1, c ≥ 0, a + b + c = n
But, then (3) fails for i = 0
uv0w = uw = 0a0c1n = 0a + c1n ∉ L, since a + c ≠ n.

UNIT-2 (REGULAR LANGUAGES)
Regular Expression
- The language accepted by finite automata can be easily described by simple expressions called Regular Expressions. It is the most effective way to represent any language.
- The languages accepted by some regular expression are referred to as Regular languages.
- A regular expression can also be described as a sequence of pattern that defines a string.
- Regular expressions are used to match character combinations in strings. String searching algorithm used this pattern to find the operations on a string.
In a regular expression, x* means zero or more occurrence of x. It can generate {e, x, xx, xxx, xxxx, .....}
In a regular expression, x+ means one or more occurrence of x. It can generate {x, xx, xxx, xxxx, .....}
Operations on Regular Language
The various operations on regular language are:Union: If L and M are two regular languages then their union L U M is also a union.
Intersection: If L and M are two regular languages then their intersection is also an intersection.
Kleen closure: If L is a regular language then its Kleen closure L1* will also be a regular language.
Example 1:
Write the regular expression for the language accepting all combinations of a's, over the set ∑ = {a}Solution:
All combinations of a's means a may be zero, single, double and so on. If a is appearing zero times, that means a null string. That is we expect the set of {ε, a, aa, aaa, ....}. So we give a regular expression for this as:
That is Kleen closure of a.
Example 2:
Write the regular expression for the language accepting all combinations of a's except the null string, over the set ∑ = {a}Solution:
The regular expression has to be built for the language
This set indicates that there is no null string. So we can denote regular expression as:
Example 3:
Write the regular expression for the language accepting all the string containing any number of a's and b's.Solution:
The regular expression will be:
This will give the set as L = {ε, a, aa, b, bb, ab, ba, aba, bab, .....}, any combination of a and b.
The (a + b)* shows any combination with a and b even a null string.
Some RE Examples
Regular Sets
Any set that represents the value of the Regular Expression is called a Regular Set.Properties of Regular Sets
Property 1. The union of two regular set is regular.Proof −
Let us take two regular expressions
RE1 = a(aa)* and RE2 = (aa)*
So, L1 = {a, aaa, aaaaa,.....} (Strings of odd length excluding Null)and L2 ={ ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∪ L2 = { ε, a, aa, aaa, aaaa, aaaaa, aaaaaa,.......}
(Strings of all possible lengths including Null)
RE (L1 ∪ L2) = a* (which is a regular expression itself)
Hence, proved.Property 2. The intersection of two regular set is regular.
Proof −
Let us take two regular expressions
RE1 = a(a*) and RE2 = (aa)*
So, L1 = { a,aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 ∩ L2 = { aa, aaaa, aaaaaa,.......} (Strings of even length excluding Null)
RE (L1 ∩ L2) = aa(aa)* which is a regular expression itself.
Hence, proved.Property 3. The complement of a regular set is regular.
Proof −
Let us take a regular expression −
RE = (aa)*
So, L = {ε, aa, aaaa, aaaaaa, .......} (Strings of even length including Null)Complement of L is all the strings that is not in L.
So, L’ = {a, aaa, aaaaa, .....} (Strings of odd length excluding Null)
RE (L’) = a(aa)* which is a regular expression itself.
Hence, proved.Property 4. The difference of two regular set is regular.
Proof −
Let us take two regular expressions −
RE1 = a (a*) and RE2 = (aa)*
So, L1 = {a, aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)
L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)
L1 – L2 = {a, aaa, aaaaa, aaaaaaa, ....}
(Strings of all odd lengths excluding Null)
RE (L1 – L2) = a (aa)* which is a regular expression.
Hence, proved.Property 5. The reversal of a regular set is regular.
Proof −
We have to prove LR is also regular if L is a regular set.
Let, L = {01, 10, 11, 10}
RE (L) = 01 + 10 + 11 + 10
LR = {10, 01, 11, 01}
RE (LR) = 01 + 10 + 11 + 10 which is regular
Hence, proved.Property 6. The closure of a regular set is regular.
Proof −
If L = {a, aaa, aaaaa, .......} (Strings of odd length excluding Null)
i.e., RE (L) = a (aa)*
L* = {a, aa, aaa, aaaa , aaaaa,……………} (Strings of all lengths excluding Null)
RE (L*) = a (a)*Hence, proved.
Property 7. The concatenation of two regular sets is regular.
Proof −
Let RE1 = (0+1)*0 and RE2 = 01(0+1)*
Here, L1 = {0, 00, 10, 000, 010, ......} (Set of strings ending in 0)
and L2 = {01, 010,011,.....} (Set of strings beginning with 01)
Then, L1 L2 = {001,0010,0011,0001,00010,00011,1001,10010,.............}
Set of strings containing 001 as a substring which can be represented by an RE − (0 + 1)*001(0 + 1)*
Hence, proved.
Identities Related to Regular Expressions
Given R, P, L, Q as regular expressions, the following identities hold −- ∅* = ε
- ε* = ε
- RR* = R*R
- R*R* = R*
- (R*)* = R*
- RR* = R*R
- (PQ)*P =P(QP)*
- (a+b)* = (a*b*)* = (a*+b*)* = (a+b*)* = a*(ba*)*
- R + ∅ = ∅ + R = R (The identity for union)
- R ε = ε R = R (The identity for concatenation)
- ∅ L = L ∅ = ∅ (The annihilator for concatenation)
- R + R = R (Idempotent law)
- L (M + N) = LM + LN (Left distributive law)
- (M + N) L = ML + NL (Right distributive law)
- ε + RR* = ε + R*R = R*
Conversion of RE to FA
To convert the RE to FA, we are going to use a method called the subset method. This method is used to obtain FA from the given regular expression. This method is given below:Step 1: Design a transition diagram for given regular expression, using NFA with ε moves.
Step 2: Convert this NFA with ε to NFA without ε.
Step 3: Convert the obtained NFA to equivalent DFA.
Example 1:
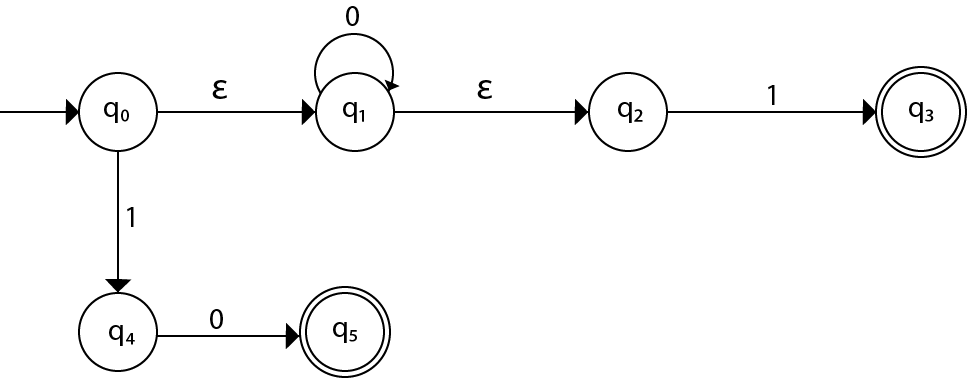
Design a FA from given regular expression 10 + (0 + 11)0* 1.Solution: First we will construct the transition diagram for a given regular expression.
Step 1:
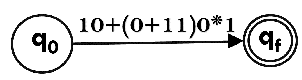
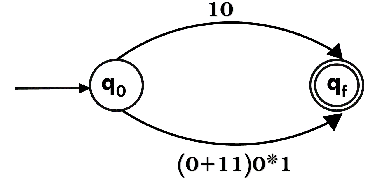
Step 2:

Step 3:

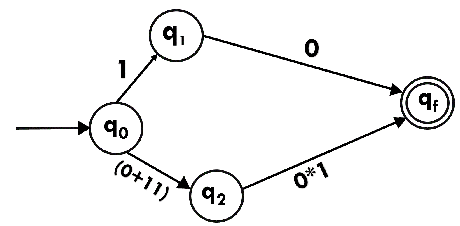
Step 4:

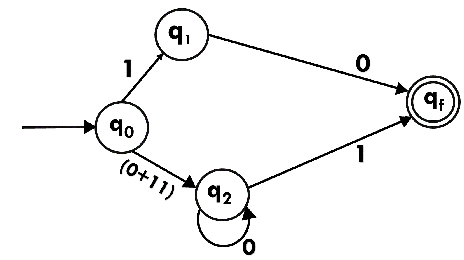
Step 5:

Now we have got NFA without ε. Now we will convert it into required DFA for that, we will first write a transition table for this NFA.
The equivalent DFA will be:
Example 2:
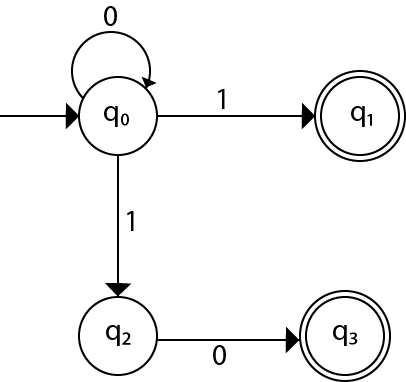
Design a NFA from given regular expression 1 (1* 01* 01*)*.Solution: The NFA for the given regular expression is as follows:
Step 1:
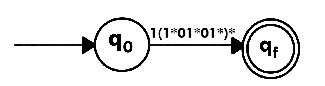
Step 2:

Step 3:

Example 3:
Construct the FA for regular expression 0*1 + 10.Solution:
We will first construct FA for R = 0*1 + 10 as follows:
Step 1:
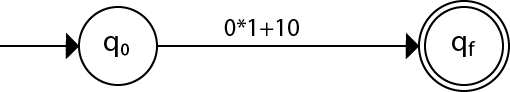
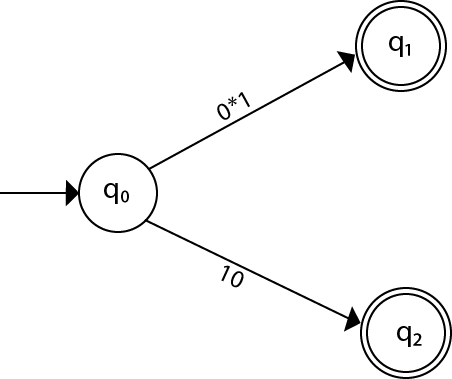
Step 2:

Step 3:

Step 4:

Arden’s Theorem in Theory of Computation
“If P and Q are two regular expressions over
That means, whenever we get any equation in the form of R = Q + RP, then we can directly replaced by R = QP*. So, here first we will prove that R = QP* is the solution of this equation and then we will also prove that it is the unique solution of this equation.
Let’s start by taking this equation as equation (i)
Now, replacing R by R = QP*, we get,
Taking Q as common,
(As we know that
Thus, R = QP* is the solution of the equation R = Q + RP.
Now, we have to prove that this is the only solution of this equation. Let me take this equation again:
Now, replace R by R = Q + RP,
Again, replace R by R = Q + RP:-
Now, replace R by R = QP*, we get,
Taking Q as common,
Hence proved.
Thus, R = QP* is the unique solution of the equation R = Q + RP.
To understand this theorem, we will solve an example:
Example –
Now,
[Applying Arden’s theorem]. Hence, the value of q2 is 0*10*.
DFA Minimization using Myhill-Nerode Theorem
Algorithm
Input − DFAOutput − Minimized DFA
Step 1 − Draw a table for all pairs of states (Qi, Qj) not necessarily connected directly [All are unmarked initially]
Step 2 − Consider every state pair (Qi, Qj) in the DFA where Qi ∈ F and Qj ∉ F or vice versa and mark them. [Here F is the set of final states]
Step 3 − Repeat this step until we cannot mark anymore states −
If there is an unmarked pair (Qi, Qj), mark it if the pair {δ (Qi, A), δ (Qi, A)} is marked for some input alphabet.
Step 4 − Combine all the unmarked pair (Qi, Qj) and make them a single state in the reduced DFA.
Example
Let us use Algorithm 2 to minimize the DFA shown below. Step 1 − We draw a table for all pair of states.
Step 1 − We draw a table for all pair of states.Step 2 − We mark the state pairs.
Step 3 − We will try to mark the state pairs, with green colored check mark, transitively. If we input 1 to state ‘a’ and ‘f’, it will go to state ‘c’ and ‘f’ respectively. (c, f) is already marked, hence we will mark pair (a, f). Now, we input 1 to state ‘b’ and ‘f’; it will go to state ‘d’ and ‘f’ respectively. (d, f) is already marked, hence we will mark pair (b, f).
After step 3, we have got state combinations {a, b} {c, d} {c, e} {d, e} that are unmarked.
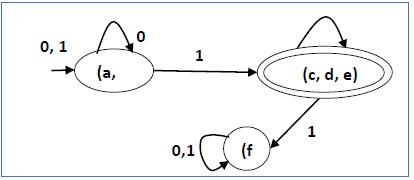
We can recombine {c, d} {c, e} {d, e} into {c, d, e}
Hence we got two combined states as − {a, b} and {c, d, e}
So the final minimized DFA will contain three states {f}, {a, b} and {c, d, e}

DFA Minimization using Equivalence Theorem
If X and Y are two states in a DFA, we can combine these two states into {X, Y} if they are not distinguishable. Two states are distinguishable, if there is at least one string S, such that one of δ (X, S) and δ (Y, S) is accepting and another is not accepting. Hence, a DFA is minimal if and only if all the states are distinguishable.Algorithm 3
Step 1 − All the states Q are divided in two partitions − final states and non-final states and are denoted by P0. All the states in a partition are 0th equivalent. Take a counter k and initialize it with 0.Step 2 − Increment k by 1. For each partition in Pk, divide the states in Pk into two partitions if they are k-distinguishable. Two states within this partition X and Y are k-distinguishable if there is an input S such that δ(X, S) and δ(Y, S) are (k-1)-distinguishable.
Step 3 − If Pk ≠ Pk-1, repeat Step 2, otherwise go to Step 4.
Step 4 − Combine kth equivalent sets and make them the new states of the reduced DFA.
Example
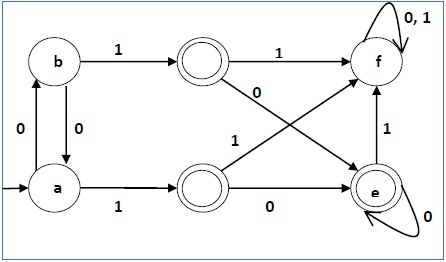
Let us consider the following DFA −
Let us apply the above algorithm to the above DFA −
- P0 = {(c,d,e), (a,b,f)}
- P1 = {(c,d,e), (a,b),(f)}
- P2 = {(c,d,e), (a,b),(f)}
There are three states in the reduced DFA. The reduced DFA is as follows −

Pumping Lemma in Theory of Computation
1. Regular Languages, and
2. Context – Free Languages
Pumping Lemma for Regular Languages
For any regular language L, there exists an integer n, such that for all x ∈ L with |x| ≥ n, there exists u, v, w ∈ Σ∗, such that x = uvw, and(1) |uv| ≤ n
(2) |v| ≥ 1
(3) for all i ≥ 0: uviw ∈ L
In simple terms, this means that if a string v is ‘pumped’, i.e., if v is inserted any number of times, the resultant string still remains in L.
Pumping Lemma is used as a proof for irregularity of a language. Thus, if a language is regular, it always satisfies pumping lemma. If there exists at least one string made from pumping which is not in L, then L is surely not regular.
The opposite of this may not always be true. That is, if Pumping Lemma holds, it does not mean that the language is regular.

For example, let us prove L01 = {0n1n | n ≥ 0} is irregular.
Let us assume that L is regular, then by Pumping Lemma the above given rules follow.
Now, let x ∈ L and |x| ≥ n. So, by Pumping Lemma, there exists u, v, w such that (1) – (3) hold.
We show that for all u, v, w, (1) – (3) does not hold.
If (1) and (2) hold then x = 0n1n = uvw with |uv| ≤ n and |v| ≥ 1.
So, u = 0a, v = 0b, w = 0c1n where : a + b ≤ n, b ≥ 1, c ≥ 0, a + b + c = n
But, then (3) fails for i = 0
uv0w = uw = 0a0c1n = 0a + c1n ∉ L, since a + c ≠ n.




0 Comments